Nonlinear Model Predictive Control with C-GMRES

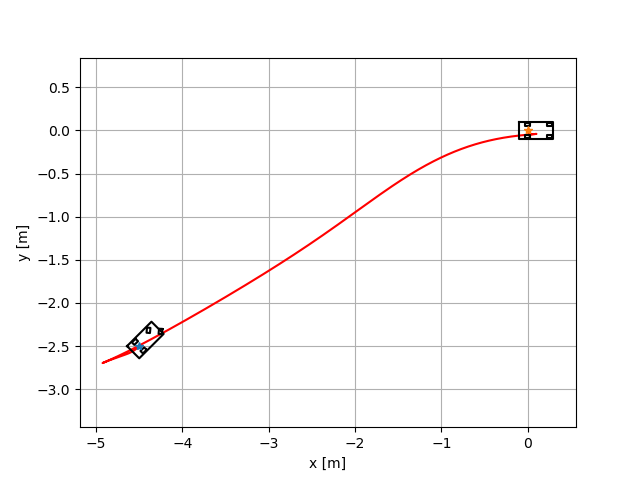
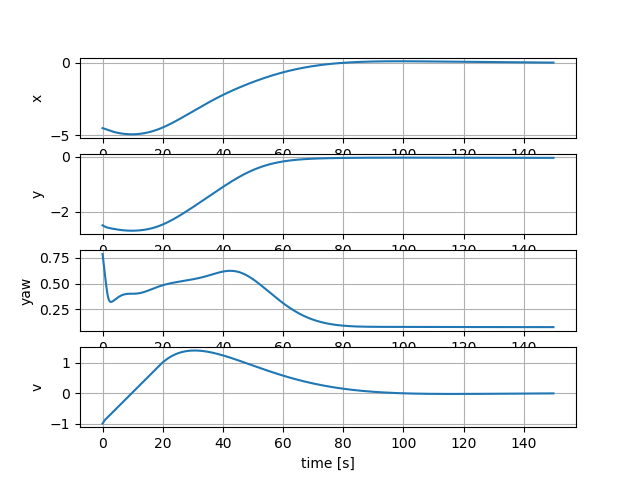
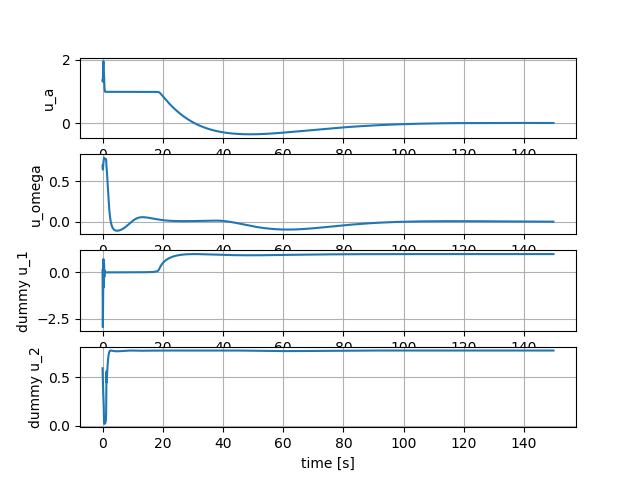
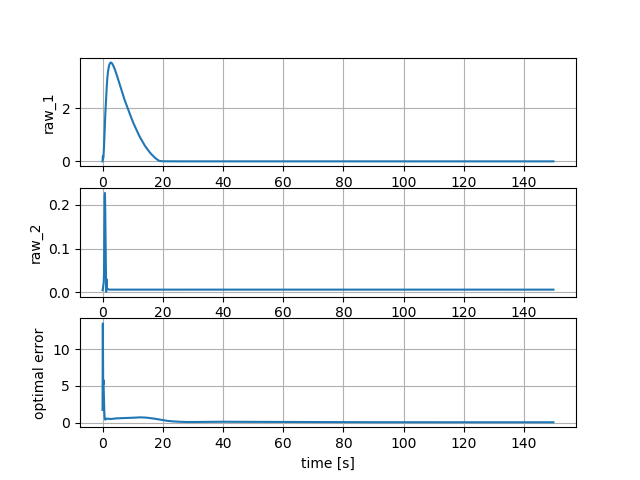
../../../_images/cgmres_nmpc_1_0.png ../../../_images/cgmres_nmpc_2_0.png ../../../_images/cgmres_nmpc_3_0.png ../../../_images/cgmres_nmpc_4_0.png
gif

Mathematical Formulation

Motion model is

\[\dot{x}=vcos\theta\]
\[\dot{y}=vsin\theta\]
\[\dot{\theta}=\frac{v}{WB}sin(u_{\delta})\]

(tan is not good for optimization)

\[\dot{v}=u_a\]

Cost function is

\[J=\frac{1}{2}(u_a^2+u_{\delta}^2)-\phi_a d_a-\phi_\delta d_\delta\]

Input constraints are

\[|u_a| \leq u_{a,max}\]
\[|u_\delta| \leq u_{\delta,max}\]

So, Hamiltonian　is

\[\begin{split}J=\frac{1}{2}(u_a^2+u_{\delta}^2)-\phi_a d_a-\phi_\delta d_\delta\\ +\lambda_1vcos\theta+\lambda_2vsin\theta+\lambda_3\frac{v}{WB}sin(u_{\delta})+\lambda_4u_a\\ +\rho_1(u_a^2+d_a^2+u_{a,max}^2)+\rho_2(u_\delta^2+d_\delta^2+u_{\delta,max}^2)\end{split}\]

Partial differential equations of the Hamiltonian are:

\(\begin{equation*} \frac{\partial H}{\partial \bf{x}}=\\ \begin{bmatrix} \frac{\partial H}{\partial x}= 0&\\ \frac{\partial H}{\partial y}= 0&\\ \frac{\partial H}{\partial \theta}= -\lambda_1vsin\theta+\lambda_2vcos\theta&\\ \frac{\partial H}{\partial v}=-\lambda_1cos\theta+\lambda_2sin\theta+\lambda_3\frac{1}{WB}sin(u_{\delta})&\\ \end{bmatrix} \\ \end{equation*}\)

\(\begin{equation*} \frac{\partial H}{\partial \bf{u}}=\\ \begin{bmatrix} \frac{\partial H}{\partial u_a}= u_a+\lambda_4+2\rho_1u_a&\\ \frac{\partial H}{\partial u_\delta}= u_\delta+\lambda_3\frac{v}{WB}cos(u_{\delta})+2\rho_2u_\delta&\\ \frac{\partial H}{\partial d_a}= -\phi_a+2\rho_1d_a&\\ \frac{\partial H}{\partial d_\delta}=-\phi_\delta+2\rho_2d_\delta&\\ \end{bmatrix} \\ \end{equation*}\)

Ref