Linear–quadratic regulator (LQR) speed and steering control
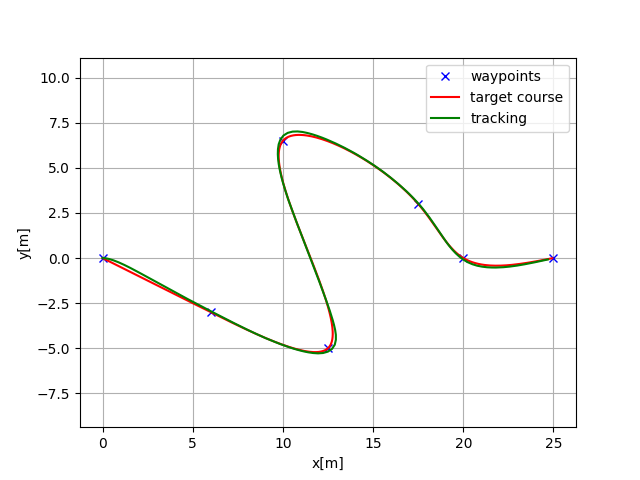
Path tracking simulation with LQR speed and steering control.
Overview
The LQR (Linear Quadratic Regulator) speed and steering control model implemented in lqr_speed_steer_control.py provides a simulation for an autonomous vehicle to track:
A desired speed by adjusting acceleration based on feedback from the current state and the desired speed.
A desired trajectory by adjusting steering angle based on feedback from the current state and the desired trajectory.
by only using one LQT controller.
Vehicle motion Model
The below figure shows the geometric model of the vehicle used in this simulation:
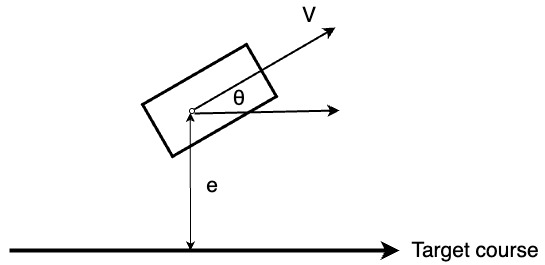
The e, \({\theta}\), and \(\upsilon\) represent the lateral error, orientation error, and velocity error, respectively, with respect to the desired trajectory and speed. And \(\dot{e}\) and \(\dot{\theta}\) represent the rates of change of these errors.
The \(e_t\) and \(\theta_t\), and \(\upsilon\) are the updated values of e, \(\theta\), \(\upsilon\) and at time t, respectively, and can be calculated using the following kinematic equations:
Where dt is the time difference and \(a_t\) is the acceleration at the time t.
The change rate of the e can be calculated as:
Where V is the current vehicle speed.
If the \(\theta\) is small,
the \(\sin(\theta)\) can be approximated as \(\theta\):
So, the change rate of the e can be approximated as:
The change rate of the \(\theta\) can be calculated as:
where L is the wheelbase of the vehicle and \(\delta\) is the steering angle.
If the \(\delta\) is small,
the \(\tan(\delta)\) can be approximated as \(\delta\):
So, the change rate of the \(\theta\) can be approximated as:
The above equations can be used to update the state of the vehicle at each time step.
Control Model
To formulate the state-space representation of the vehicle dynamics as a linear model, the state vector x and control input vector u are defined as follows:
The linear state transition equation can be represented as:
where:
\(\begin{equation*} A = \begin{bmatrix} 1 & dt & 0 & 0 & 0\\ 0 & 0 & v & 0 & 0\\ 0 & 0 & 1 & dt & 0\\ 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1\\\end{bmatrix} \end{equation*}\)
\(\begin{equation*} B = \begin{bmatrix} 0 & 0\\ 0 & 0\\ 0 & 0\\ \frac{v}{L} & 0\\ 0 & dt \\ \end{bmatrix} \end{equation*}\)
LQR controller
The Linear Quadratic Regulator (LQR) controller is used to calculate the optimal control input u that minimizes the quadratic cost function:
\(J = \sum_{t=0}^{N} (x_t^T Q x_t + u_t^T R u_t)\)
where Q and R are the weighting matrices for the state and control input, respectively.
for the linear model:
\(x_{t+1} = A x_t + B u_t\)
The optimal control input u can be calculated as:
\(u_t = -K x_t\)
where K is the feedback gain matrix obtained by solving the Riccati equation.
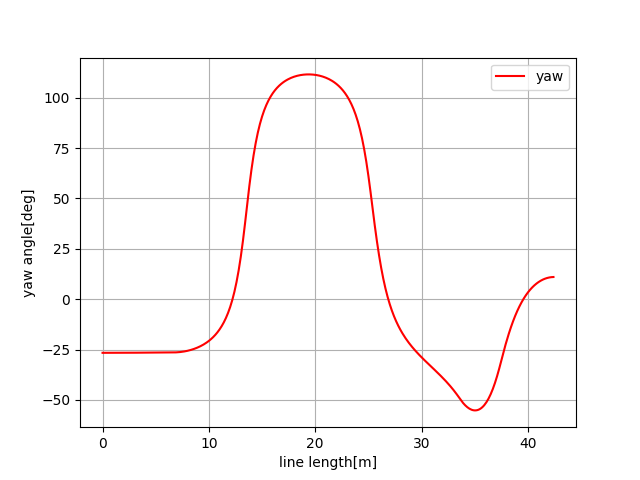
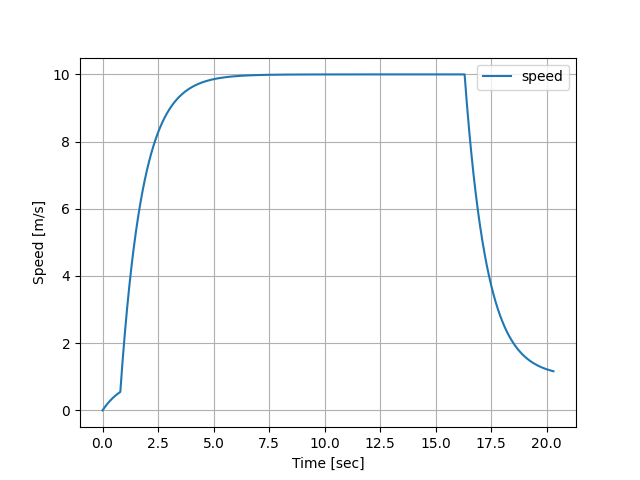
Simulation results