Extended Kalman Filter Localization

Position Estimation Kalman Filter

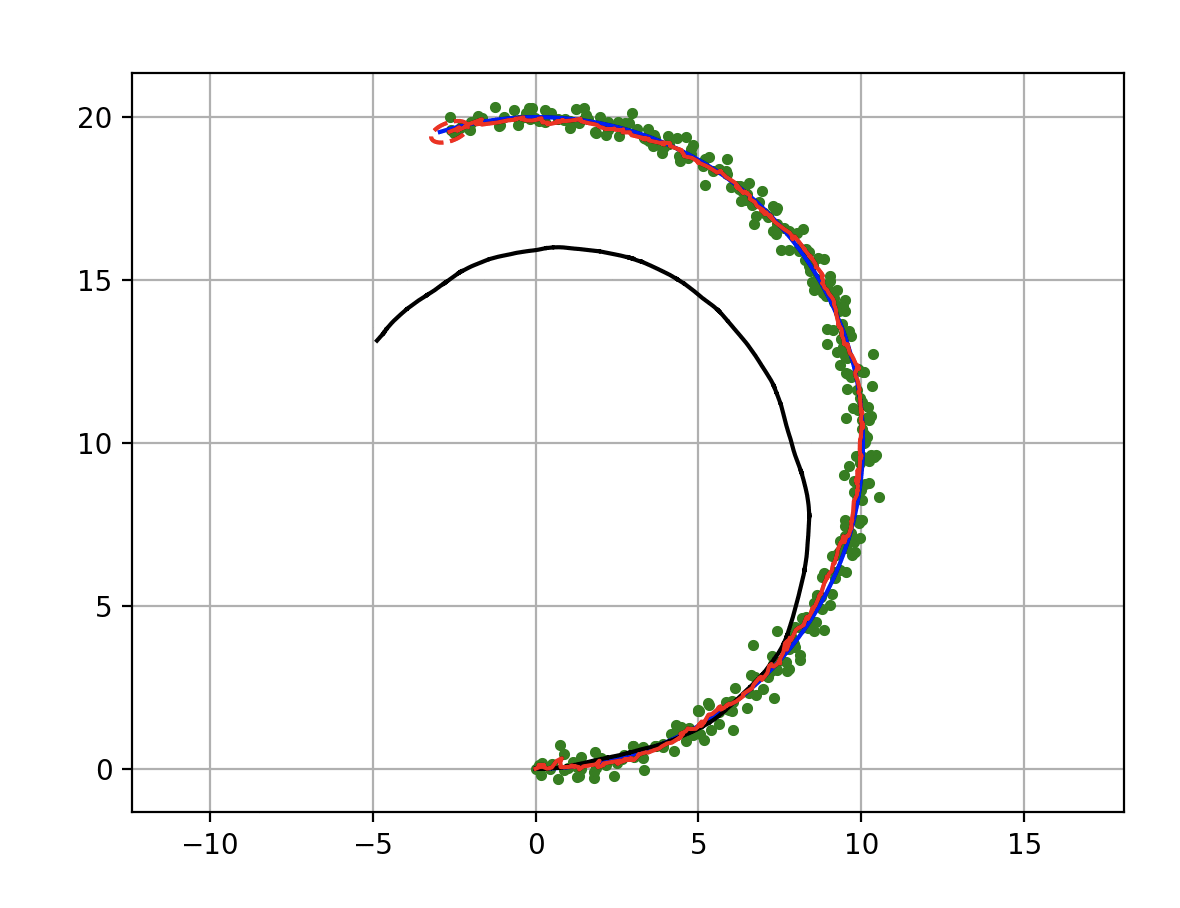
This is a sensor fusion localization with Extended Kalman Filter(EKF).

The blue line is true trajectory, the black line is dead reckoning trajectory,

the green point is positioning observation (ex. GPS), and the red line is estimated trajectory with EKF.

The red ellipse is estimated covariance ellipse with EKF.

Code Link

Localization.extended_kalman_filter.extended_kalman_filter.ekf_estimation(xEst, PEst, z, u)

Extended Kalman Filter algorithm

Localization process using Extended Kalman Filter:EKF is

=== Predict ===

\(x_{Pred} = Fx_t+Bu_t\)

\(P_{Pred} = J_f P_t J_f^T + Q\)

=== Update ===

\(z_{Pred} = Hx_{Pred}\)

\(y = z - z_{Pred}\)

\(S = J_g P_{Pred}.J_g^T + R\)

\(K = P_{Pred}.J_g^T S^{-1}\)

\(x_{t+1} = x_{Pred} + Ky\)

\(P_{t+1} = ( I - K J_g) P_{Pred}\)

Filter design

In this simulation, the robot has a state vector includes 4 states at time \(t\).

\[\textbf{x}_t=[x_t, y_t, \phi_t, v_t]\]

x, y are a 2D x-y position, \(\phi\) is orientation, and v is velocity.

In the code, “xEst” means the state vector. code

And, \(P_t\) is covariace matrix of the state,

\(Q\) is covariance matrix of process noise,

\(R\) is covariance matrix of observation noise at time \(t\)

The robot has a speed sensor and a gyro sensor.

So, the input vecor can be used as each time step

\[\textbf{u}_t=[v_t, \omega_t]\]

Also, the robot has a GNSS sensor, it means that the robot can observe x-y position at each time.

\[\textbf{z}_t=[x_t,y_t]\]

The input and observation vector includes sensor noise.

In the code, “observation” function generates the input and observation vector with noise code

Motion Model

The robot model is

\[\dot{x} = v \cos(\phi)\]

\[\dot{y} = v \sin(\phi)\]

\[\dot{\phi} = \omega\]

So, the motion model is

\[\textbf{x}_{t+1} = f(\textbf{x}_t, \textbf{u}_t) = F\textbf{x}_t+B\textbf{u}_t\]

where

\(\begin{equation*} F= \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ \end{bmatrix} \end{equation*}\)

\(\begin{equation*} B= \begin{bmatrix} cos(\phi) \Delta t & 0\\ sin(\phi) \Delta t & 0\\ 0 & \Delta t\\ 1 & 0\\ \end{bmatrix} \end{equation*}\)

\(\Delta t\) is a time interval.

This is implemented at code

The motion function is that

\(\begin{equation*} \begin{bmatrix} x' \\ y' \\ w' \\ v' \end{bmatrix} = f(\textbf{x}, \textbf{u}) = \begin{bmatrix} x + v\cos(\phi)\Delta t \\ y + v\sin(\phi)\Delta t \\ \phi + \omega \Delta t \\ v \end{bmatrix} \end{equation*}\)

Its Jacobian matrix is

\(\begin{equation*} J_f = \begin{bmatrix} \frac{\partial x'}{\partial x}& \frac{\partial x'}{\partial y} & \frac{\partial x'}{\partial \phi} & \frac{\partial x'}{\partial v}\\ \frac{\partial y'}{\partial x}& \frac{\partial y'}{\partial y} & \frac{\partial y'}{\partial \phi} & \frac{\partial y'}{\partial v}\\ \frac{\partial \phi'}{\partial x}& \frac{\partial \phi'}{\partial y} & \frac{\partial \phi'}{\partial \phi} & \frac{\partial \phi'}{\partial v}\\ \frac{\partial v'}{\partial x}& \frac{\partial v'}{\partial y} & \frac{\partial v'}{\partial \phi} & \frac{\partial v'}{\partial v} \end{bmatrix} \end{equation*}\)

\(\begin{equation*} 　= \begin{bmatrix} 1& 0 & -v \sin(\phi) \Delta t & \cos(\phi) \Delta t\\ 0 & 1 & v \cos(\phi) \Delta t & \sin(\phi) \Delta t\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \end{equation*}\)

Observation Model

The robot can get x-y position information from GPS.

So GPS Observation model is

\[\textbf{z}_{t} = g(\textbf{x}_t) = H \textbf{x}_t\]

where

\(\begin{equation*} H = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ \end{bmatrix} \end{equation*}\)

The observation function states that

\(\begin{equation*} \begin{bmatrix} x' \\ y' \end{bmatrix} = g(\textbf{x}) = \begin{bmatrix} x \\ y \end{bmatrix} \end{equation*}\)

Its Jacobian matrix is

\(\begin{equation*} J_g = \begin{bmatrix} \frac{\partial x'}{\partial x} & \frac{\partial x'}{\partial y} & \frac{\partial x'}{\partial \phi} & \frac{\partial x'}{\partial v}\\ \frac{\partial y'}{\partial x}& \frac{\partial y'}{\partial y} & \frac{\partial y'}{\partial \phi} & \frac{\partial y'}{ \partial v}\\ \end{bmatrix} \end{equation*}\)

\(\begin{equation*} 　= \begin{bmatrix} 1& 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ \end{bmatrix} \end{equation*}\)

Kalman Filter with Speed Scale Factor Correction

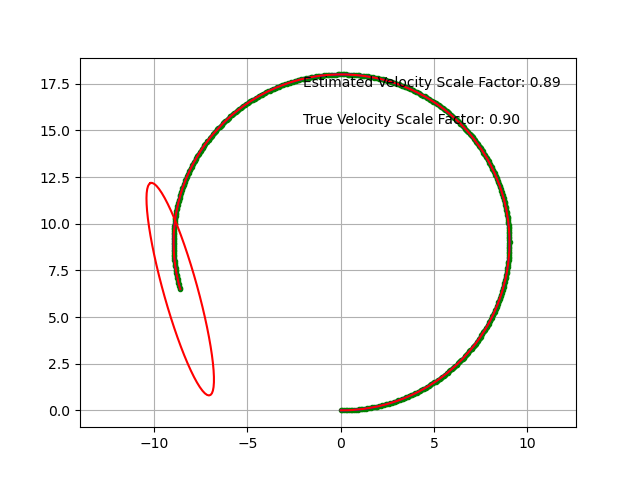
This is a Extended kalman filter (EKF) localization with velocity correction.

This is for correcting the vehicle speed measured with scale factor errors due to factors such as wheel wear.

In this simulation, the robot has a state vector includes 5 states at time \(t\).

\[\textbf{x}_t=[x_t, y_t, \phi_t, v_t, s_t]\]

x, y are a 2D x-y position, \(\phi\) is orientation, v is velocity, and s is a scale factor of velocity.

In the code, “xEst” means the state vector. code

The rest is the same as the Position Estimation Kalman Filter.

Code Link

Localization.extended_kalman_filter.ekf_with_velocity_correction.ekf_estimation(xEst, PEst, z, u)

Motion Model

The robot model is

\[\dot{x} = v s \cos(\phi)\]

\[\dot{y} = v s \sin(\phi)\]

\[\dot{\phi} = \omega\]

So, the motion model is

\[\textbf{x}_{t+1} = f(\textbf{x}_t, \textbf{u}_t) = F\textbf{x}_t+B\textbf{u}_t\]

where

\(\begin{equation*} F= \begin{bmatrix} 1 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1\\ \end{bmatrix} \end{equation*}\)

\(\begin{equation*} B= \begin{bmatrix} cos(\phi) \Delta t s & 0\\ sin(\phi) \Delta t s & 0\\ 0 & \Delta t\\ 1 & 0\\ 0 & 0\\ \end{bmatrix} \end{equation*}\)

\(\Delta t\) is a time interval.

This is implemented at code

The motion function is that

\(\begin{equation*} \begin{bmatrix} x' \\ y' \\ w' \\ v' \end{bmatrix} = f(\textbf{x}, \textbf{u}) = \begin{bmatrix} x + v s \cos(\phi)\Delta t \\ y + v s \sin(\phi)\Delta t \\ \phi + \omega \Delta t \\ v \end{bmatrix} \end{equation*}\)

Its Jacobian matrix is

\(\begin{equation*} J_f = \begin{bmatrix} \frac{\partial x'}{\partial x}& \frac{\partial x'}{\partial y} & \frac{\partial x'}{\partial \phi} & \frac{\partial x'}{\partial v} & \frac{\partial x'}{\partial s}\\ \frac{\partial y'}{\partial x}& \frac{\partial y'}{\partial y} & \frac{\partial y'}{\partial \phi} & \frac{\partial y'}{\partial v} & \frac{\partial y'}{\partial s}\\ \frac{\partial \phi'}{\partial x}& \frac{\partial \phi'}{\partial y} & \frac{\partial \phi'}{\partial \phi} & \frac{\partial \phi'}{\partial v} & \frac{\partial \phi'}{\partial s}\\ \frac{\partial v'}{\partial x}& \frac{\partial v'}{\partial y} & \frac{\partial v'}{\partial \phi} & \frac{\partial v'}{\partial v} & \frac{\partial v'}{\partial s} \\ \frac{\partial s'}{\partial x}& \frac{\partial s'}{\partial y} & \frac{\partial s'}{\partial \phi} & \frac{\partial s'}{\partial v} & \frac{\partial s'}{\partial s} \end{bmatrix} \end{equation*}\)

\(\begin{equation*} 　= \begin{bmatrix} 1& 0 & -v s \sin(\phi) \Delta t & s \cos(\phi) \Delta t & \cos(\phi) v \Delta t\\ 0 & 1 & v s \cos(\phi) \Delta t & s \sin(\phi) \Delta t & v \sin(\phi) \Delta t\\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \end{bmatrix} \end{equation*}\)

Observation Model

The robot can get x-y position information from GPS.

So GPS Observation model is

\[\textbf{z}_{t} = g(\textbf{x}_t) = H \textbf{x}_t\]

where

\(\begin{equation*} H = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ \end{bmatrix} \end{equation*}\)

The observation function states that

\(\begin{equation*} \begin{bmatrix} x' \\ y' \end{bmatrix} = g(\textbf{x}) = \begin{bmatrix} x \\ y \end{bmatrix} \end{equation*}\)

Its Jacobian matrix is

\(\begin{equation*} J_g = \begin{bmatrix} \frac{\partial x'}{\partial x} & \frac{\partial x'}{\partial y} & \frac{\partial x'}{\partial \phi} & \frac{\partial x'}{\partial v} & \frac{\partial x'}{\partial s}\\ \frac{\partial y'}{\partial x}& \frac{\partial y'}{\partial y} & \frac{\partial y'}{\partial \phi} & \frac{\partial y'}{ \partial v} & \frac{\partial y'}{ \partial s}\\ \end{bmatrix} \end{equation*}\)

\(\begin{equation*} 　= \begin{bmatrix} 1& 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0\\ \end{bmatrix} \end{equation*}\)

Reference

• PROBABILISTIC-ROBOTICS.ORG