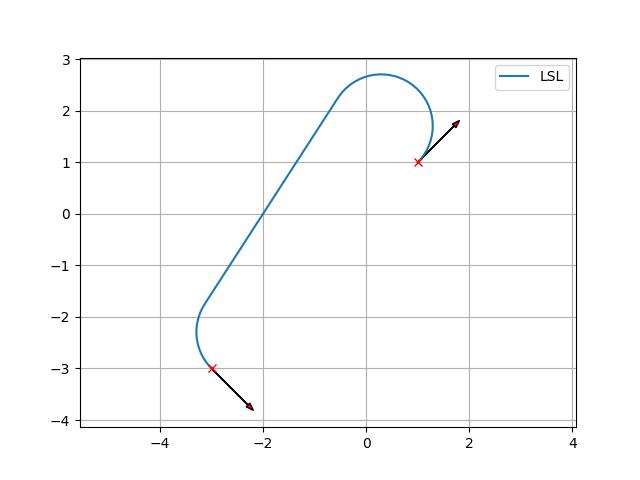
Dubins path planning

A sample code for Dubins path planning.

https://github.com/AtsushiSakai/PythonRoboticsGifs/raw/master/PathPlanning/DubinsPath/animation.gif?raw=True

Dubins path

Dubins path is a analytical path planning algorithm for a simple car model.

It can generates a shortest path between two 2D poses (x, y, yaw) with maximum curvature constraint and tangent(yaw angle) constraint.

Generated paths consist of 3 segments of maximum curvature curves or a straight line segment.

Each segment type can is categorized by 3 type: ‘Right turn (R)’ , ‘Left turn (L)’, and ‘Straight (S).’

Possible path will be at least one of these six types: RSR, RSL, LSR, LSL, RLR, LRL.

Dubins path planner can output each segment type and distance of each course segment.

For example, a RSR Dubins path is:

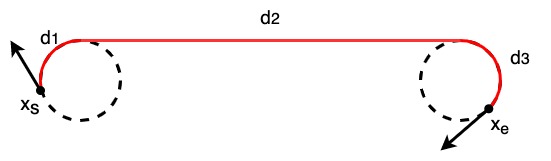
../../../_images/RSR.jpg

Each segment distance can be calculated by:

\(\alpha = mod(-\theta)\)

\(\beta = mod(x_{e, yaw} - \theta)\)

\(p^2 = 2 + d ^ 2 - 2\cos(\alpha-\beta) + 2d(\sin\alpha - \sin\beta)\)

\(t = atan2(\cos\beta - \cos\alpha, d + \sin\alpha - \sin\beta)\)

\(d_1 = mod(-\alpha + t)\)

\(d_2 = p\)

\(d_3 = mod(\beta - t)\)

where \(\theta\) is tangent and d is distance from \(x_s\) to \(x_e\)

A RLR Dubins path is:

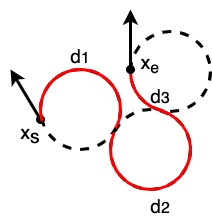
../../../_images/RLR.jpg

Each segment distance can be calculated by:

\(t = (6.0 - d^2 + 2\cos(\alpha-\beta) + 2d(\sin\alpha - \sin\beta)) / 8.0\)

\(d_2 = mod(2\pi - acos(t))\)

\(d_1 = mod(\alpha - atan2(\cos\beta - \cos\alpha, d + \sin\alpha - \sin\beta) + d_2 / 2.0)\)

\(d_3 = mod(\alpha - \beta - d_1 + d_2)\)

You can generate a path from these information and the maximum curvature information.

A path type which has minimum course length among 6 types is selected, and then a path is constructed based on the selected type and its distances.

API

PathPlanning.DubinsPath.dubins_path_planner.plan_dubins_path(s_x, s_y, s_yaw, g_x, g_y, g_yaw, curvature, step_size=0.1, selected_types=None)[source]

Plan dubins path

Parameters:

  • s_x (float) – x position of the start point [m]

  • s_y (float) – y position of the start point [m]

  • s_yaw (float) – yaw angle of the start point [rad]

  • g_x (float) – x position of the goal point [m]

  • g_y (float) – y position of the end point [m]

  • g_yaw (float) – yaw angle of the end point [rad]

  • curvature (float) – curvature for curve [1/m]

  • step_size (float (optional)) – step size between two path points [m]. Default is 0.1

  • selected_types (a list of string or None) – selected path planning types. If None, all types are used for path planning, and minimum path length result is returned. You can select used path plannings types by a string list. e.g.: [“RSL”, “RSR”]

Returns:

  • x_list (array) – x positions of the path

  • y_list (array) – y positions of the path

  • yaw_list (array) – yaw angles of the path

  • modes (array) – mode list of the path

  • lengths (array) – arrow_length list of the path segments.

Examples

You can generate a dubins path.

>>> start_x = 1.0  # [m]
>>> start_y = 1.0  # [m]
>>> start_yaw = np.deg2rad(45.0)  # [rad]
>>> end_x = -3.0  # [m]
>>> end_y = -3.0  # [m]
>>> end_yaw = np.deg2rad(-45.0)  # [rad]
>>> curvature = 1.0
>>> path_x, path_y, path_yaw, mode, _ = plan_dubins_path(
            start_x, start_y, start_yaw, end_x, end_y, end_yaw, curvature)
>>> plt.plot(path_x, path_y, label="final course " + "".join(mode))
>>> plot_arrow(start_x, start_y, start_yaw)
>>> plot_arrow(end_x, end_y, end_yaw)
>>> plt.legend()
>>> plt.grid(True)
>>> plt.axis("equal")
>>> plt.show()
../../../_images/dubins_path.jpg

Reference