Normal Distance Transform (NDT) map

This is a NDT mapping example.

Normal Distribution Transform (NDT) is a map representation that uses normal distribution for observation point modeling.

Normal Distribution

Normal distribution consists of two parameters: mean \(\mu\) and covariance \(\Sigma\).

\(\mathbf{X} \sim \mathcal{N}(\boldsymbol{\mu}, \boldsymbol{\Sigma})\)

In the 2D case, \(\boldsymbol{\mu}\) is a 2D vector and \(\boldsymbol{\Sigma}\) is a 2x2 matrix.

In the matrix form, the probability density function of thr normal distribution is:

\(X=\frac{1}{\sqrt{(2 \pi)^2|\Sigma|}} \exp \left\{-\frac{1}{2}^t(x-\mu) \sum^{-1}(x-\mu)\right\}\)

NDT mapping consists of two steps:

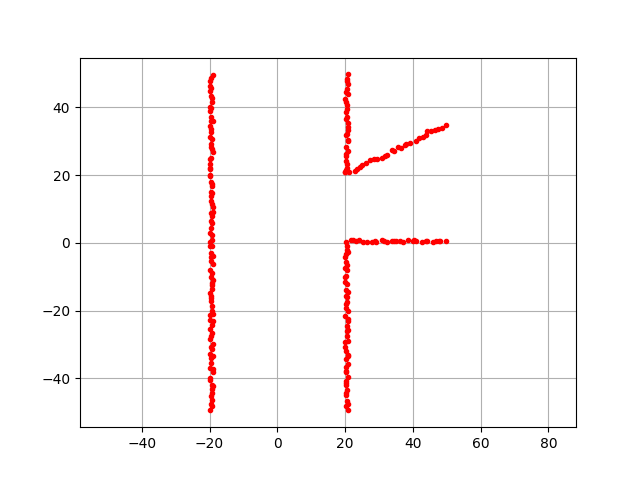
When we have a new observation like this:

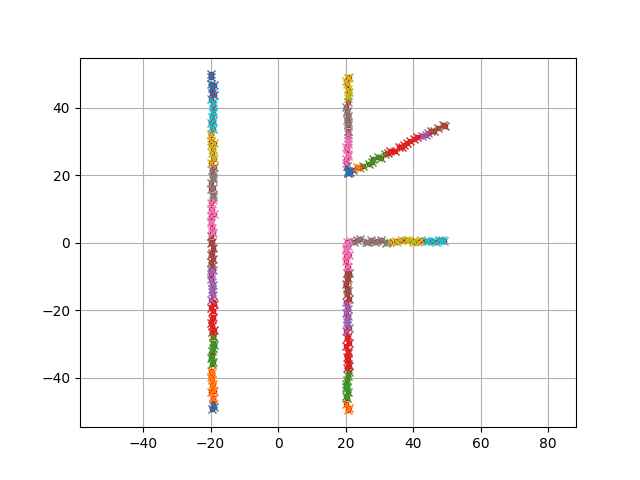
First, we need to cluster the observation points. This is done by using a grid based clustering algorithm.

The result is:

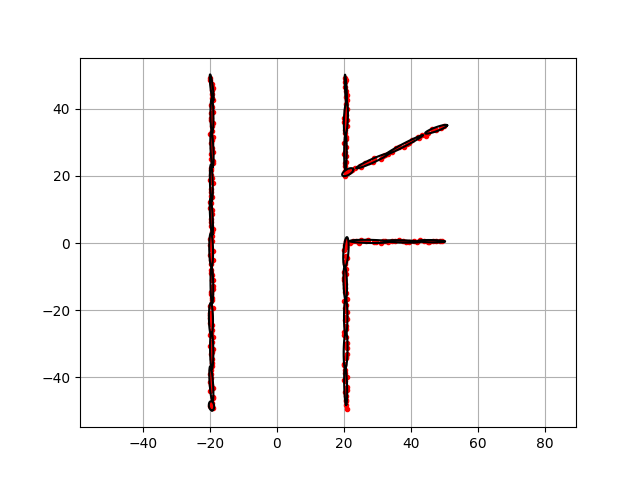
Then, we need to fit a normal distribution to each grid cluster.

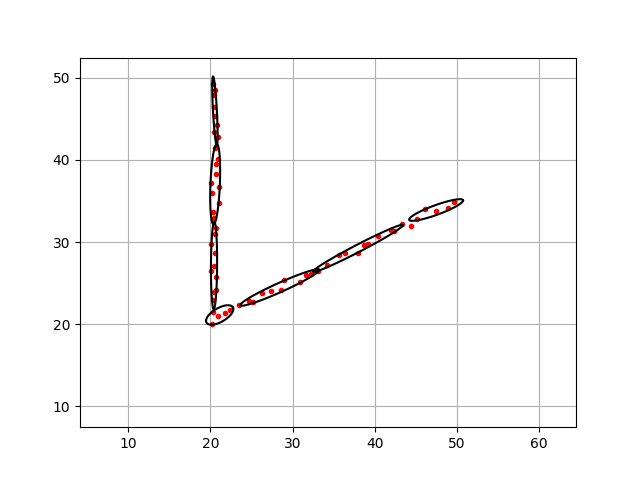
Black ellipse shows each NDT grid like this:

class Mapping.ndt_map.ndt_map.NDTMap(ox, oy, resolution)[source]

Normal Distribution Transform (NDT) map class

Parameters:

class NDTGrid[source]

NDT grid